Quantifying passing skill has been a topic that has gained greater attention over the past 18 months in public analytics circles, with Paul Riley, StatsBomb and Played off the Park regularly publishing insights from their passing models. I talked a little about my own model last season but only published results on how teams disrupted their opponents passing. I thought delving into the nuts and bolts of the model plus reporting some player-centric results would be a good place to start as I plan to write more on passing over the next few months.
Firstly, the model quantifies the difficulty of an open-play pass based on its start and end location, as well as whether it was with the foot or head. So for example, relatively short backward passes by a centre back to their goalkeeper are completed close to 100% of the time, whereas medium-range forward passes from out-wide into the centre of the penalty area have pass completion rates of around 20%.
The data used for the model is split into training and testing sets to prevent over-fitting. The Random Forest-based model does a pretty good job of representing the different components that drive pass difficulty, some of which are illustrated in the figure below (also see the appendix here for some further diagnostics).
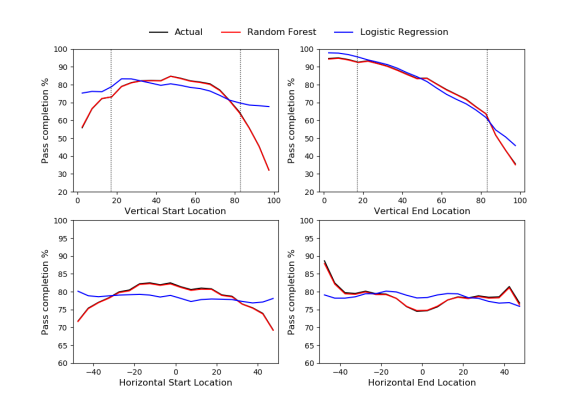
Comparison between expected pass completion rates from two different passing models and actual pass completion rates based on the start and end location of an open-play pass. The horizontal dimension is orientated from left-to-right, with zero designating the centre of the pitch. The dashed lines in the vertical dimension plots show the location of the edge of each penalty area. Data via Opta.
One slight wrinkle with the model is that it has trouble with very short passes of less than approximately 5 yards due to the way the data is collected; if a player attempts a pass and an opponent in his immediate vicinity blocks it, then the pass is unsuccessful and makes it looks like such passes are really hard, even though the player was actually attempting a much longer pass. Neil Charles reported something similar in his OptaPro Forum presentation in 2017. For the rest of the analysis, such passes are excluded.
None shall pass
That gets some of the under-the-hood stuff out of the way, so let’s take a look at ways of quantifying passing ‘skill’.
Similar to the concept of expected goals, the passing model provides a numerical likelihood of a given pass being completed by an average player; deviations from this expectation in reality may point to players with greater or less ‘skill’ at passing. The analogous concept from expected goals would be comparing the number of goals scored versus expectation and interpreting this as ‘finishing skill‘ or lack there of. However, when it comes to goal-scoring, such interpretations tend to be very uncertain due to significant sample size issues because shots and goals are relatively infrequent occurrences. This is less of a concern when it comes to passing though, as many players will often attempt more passes in a season than they would take shots in their entire career.
Another basic output of such models is an indication of how adventurous a player is in their passing – are they playing lots of simple sideways passes or are they regularly attempting defense-splitting passes?
The figure below gives a broad overview of these concepts for out-field players from the top-five leagues (England, France, Germany, Italy and Spain) over the past two seasons. Only passes with the feet are included in the analysis.
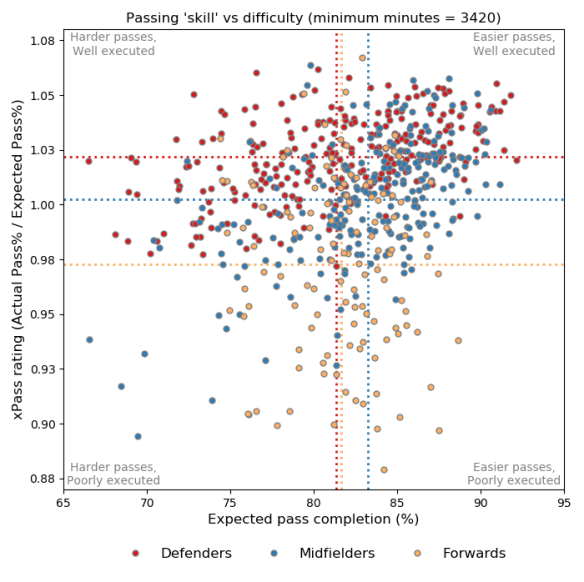
Passing ‘skill’ compared to pass difficulty for outfield players from the past two seasons in the big-five leagues, with each data point representing a player who played more than 3420 minutes (equivalent to 38 matches) over the period. The dashed lines indicate the average values across each position. Foot-passes only. Data from Opta.
One of the things that is clear when examining the data is that pulling things apart by position is important as the model misses some contextual factors and player roles obviously vary a huge amount depending on their position. The points in the figure are coloured according to basic position profiles (I could be more nuanced here but I’ll keep it simpler for now), with the dashed lines showing the averages for each position.
In terms of pass difficulty, midfielders attempt the easiest passes with an average expected completion of 83.2%. Forwards (81.6%) attempt slightly easier passes than defenders (81.4%), which makes sense to me when compared to midfielders, as the former are often going for tough passes in the final third, while the latter are playing more long passes and crosses.
Looking at passing skill is interesting, as it suggest that the average defender is actually more skilled than the average midfielder?!? While the modern game requires defenders to be adept in possession, I’m unconvinced that their passing skills outstrip midfielders. What I suspect is happening is that passes by defenders are being rated as slightly harder than they are in reality due to the model not knowing about defensive pressure, which on average will be less for defenders than midfielders.
Forwards are rated worst in terms of passing skill, which is probably again a function of the lack of defensive pressure included as a variable, as well as other skills being more-valued for forwards than passing e.g. goal-scoring, dribbling, aerial-ability.
Pass muster
Now we’ve got all that out of the way, here are some lists separated by position. I don’t watch anywhere near as much football as I once did, so really can’t comment on quite a few of these and am open to feedback.
Note the differences between the players on these top-ten lists are tiny, so the order is pretty arbitrary and there are lots of other players that the model thinks are great passers who just missed the cut.
First-up, defenders: *shrugs*.
In terms of how I would frame this, I wouldn’t say ‘Faouzi Ghoulam is the best passer out of defenders in the big-five leagues’. Instead I would go for something along the lines of ‘Faouzi Ghoulam’s passing stands out and he is among the best left-backs according to the model’. The latter is more consistent with how football is talked about in a ‘normal’ environment, while also being a more faithful presentation of the model.
Looking at the whole list, there is quite a range of pass difficulty, with full-backs tending to play more difficult passes (passes into the final third, crosses into the penalty area) and the model clearly rates good-crossers like Ghoulam, Baines and Valencia. Obviously that is a very different skill-set to what you would look for in a centre back, so filtering the data more finely is an obvious next step.
Defenders (* denotes harder than average passes)
| Name | Team | xP rating | Pass difficulty |
| Faouzi Ghoulam | Napoli | 1.06 | 80.3* |
| Leighton Baines | Everton | 1.06 | 76.5* |
| Stefan Radu | Lazio | 1.06 | 82.1 |
| Thiago Silva | PSG | 1.06 | 91.0 |
| Benjamin Hübner | Hoffenheim | 1.05 | 84.4 |
| Mats Hummels | Bayern Munich | 1.05 | 86.0 |
| Kevin Vogt | Hoffenheim | 1.05 | 87.4 |
| César Azpilicueta | Chelsea | 1.05 | 83.4 |
| Kalidou Koulibaly | Napoli | 1.05 | 87.8 |
| Antonio Valencia | Manchester United | 1.05 | 80.0* |
On to midfielders: I think this looks pretty reasonable with some well-known gifted passers making up the list, although I’m a little dubious about Dembélé and Fernandinho being quite this high up. Iwobi is an interesting one and will keep James Yorke happy.
Fàbregas stands-out due to his pass difficulty being well-below average without having a cross-heavy profile – nobody gets near him for the volume of difficult passes he completes.
Midfielders (* denotes harder than average passes)
| Name | Team | xP rating | Pass difficulty |
| Cesc Fàbregas | Chelsea | 1.06 | 79.8* |
| Toni Kroos | Real Madrid | 1.06 | 88.1 |
| Luka Modric | Real Madrid | 1.06 | 85.9 |
| Arjen Robben | Bayern Munich | 1.05 | 79.6* |
| Jorginho | Napoli | 1.05 | 86.8 |
| Mousa Dembélé | Tottenham Hotspur | 1.05 | 89.9 |
| Fernandinho | Manchester City | 1.05 | 87.2 |
| Marco Verratti | PSG | 1.05 | 87.3 |
| Alex Iwobi | Arsenal | 1.05 | 84.9 |
| Juan Mata | Manchester United | 1.05 | 84.5 |
Finally, forwards AKA ‘phew, it thinks Messi is amazing’.
Özil is the highest-rated player across the dataset, which is driven by his ability to retain possession and create in the final third. Like Fàbregas above, Messi stands out for the difficulty of the passes he attempts and that he is operating in the congested central and half-spaces in the final third, where mere mortals (and the model) tend to struggle.
In terms of surprising names: Alejandro Gomez appears to be very good at crossing, while City’s meep-meep wide forwards being so far up the list makes we wonder about team-effects.
Also, I miss Philippe Coutinho.
Forwards (* denotes harder than average passes)
| Name | Team | xP rating | Pass difficulty |
| Mesut Özil | Arsenal | 1.07 | 82.9 |
| Eden Hazard | Chelsea | 1.05 | 81.9 |
| Lionel Messi | Barcelona | 1.05 | 79.4* |
| Philippe Coutinho | Liverpool | 1.04 | 80.6* |
| Paulo Dybala | Juventus | 1.03 | 84.8 |
| Alejandro Gomez | Atalanta | 1.03 | 74.4* |
| Raheem Sterling | Manchester City | 1.03 | 81.6* |
| Leroy Sané | Manchester City | 1.03 | 81.9 |
| Lorenzo Insigne | Napoli | 1.03 | 84.3 |
| Diego Perotti | Roma | 1.02 | 78.4* |
Finally, the answer to what everyone really wants to know is, who is the worst passer? Step-forward Mario Gómez – I guess he made the right call when he pitched his tent in the heart of the penalty area.
Pass it on
While this kind of analysis can’t replace detailed video and live scouting for an individual, I think it can provide a lot of value. Traditional methods can’t watch every pass by every player across a league but data like this can. However, there is certaintly a lot of room for improvement and further analysis.
A few things I particularly want to work on are:
- Currently there is no information in the model about the type of attacking move that is taking place, which could clearly influence pass difficulty e.g. a pass during a counter-attacking situation or one within a long passing-chain with much slower build-up. Even if you didn’t include such parameters in the model, it would be a nice means of filtering different pass situations.
- Another element in terms of context is attempting a pass after a dribble, especially given some of the ratings above e.g. Hazard and Dembélé. I can envisage the model somewhat conflates the ability to create space through dribbling and passing skill (although this isn’t necessarily a bad thing depending on what you want to assess).
- Average difficulty is a bit of a blunt metric and hides a lot of information. Developing this area should be a priority for more detailed analysis as I think building a profile of a player’s passing tendencies would be a powerful tool.
- You’ll have probably noticed the absence of goalkeepers in the results above. I’ve left them alone for now as the analysis tends to assign very high skill levels to some goalkeepers, especially those attempting lots of long passes. My suspicion is that long balls up-field that are successfully headed by a goalkeeper’s team-mate are receiving a bit too much credit i.e. yes the pass was ‘successful’ but that doesn’t always mean that possession was retained after the initial header. That isn’t necessarily the fault of the goalkeeper, who is generally adhering to the tactics of their team and the match situation but I’m not sure it really reflects what we envisage as passing ‘skill’ when it comes to goalkeepers. Discriminating between passes to feet and aerial balls would be a useful addition to the analysis here.
- Using minutes as the cut-off for the skill ratings leaves a lot of information on the table. The best and worst passers can be pretty reliably separated after just a few hundred passes e.g. Ruben Loftus-Cheek shows up as an excellent passer after just ~2000 minutes in the Premier League. Being able to quickly assess young players and new signings should be possible. Taking into account the number of passes a player makes should also be used to assess the uncertainty in the ratings.
I’ve gone on enough about this, so I’ll finish by saying that any feedback on the analysis and ratings is welcome. To facilitate that, I’ve built a Tableau dashboard that you can mess around with that is available from here and you can find the raw data here.
Time to pass and move.