Following my previous article on the shot-stopping ability of goalkeepers, Mike Goodman posed an interesting question on Twitter:
This is certainly not an annoying question and I tend to think that such questions should be encouraged in the analytics community. Greater discussion should stimulate further work and enrich the community.
It certainly stands to reason and observation that goalkeepers can influence a strikers options and decision-making when shooting but extracting robust signals of such a skill may prove problematic.
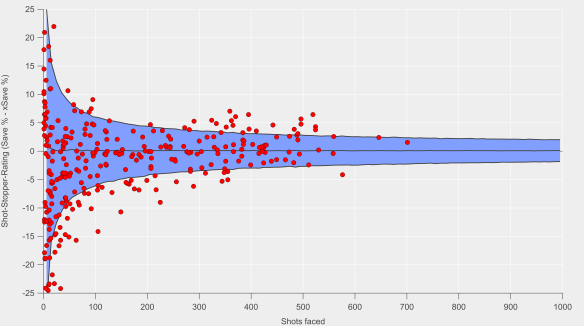
To try and answer this question, I built a quick model to calculate the likelihood that a non-blocked shot would end up on target. It’s essentially the same model as in my previous post but for expected shots on target rather than goals. The idea behind the model is that goalkeepers who are able to ‘force’ shots off-target would have a net positive rating when subtracting actual shots on target from the expected rate.
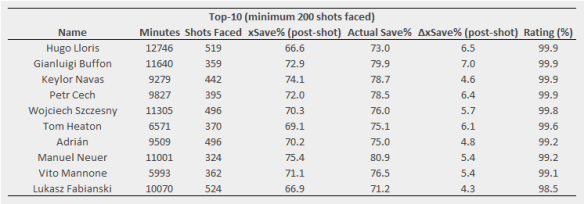
When I looked at the results, two of the standout names were Gianluigi Buffon and Jan Oblak; Buffon is a legend of the game and up there with the best of all time, while Oblak is certainly well regarded, so not a bad start.
However, after delving a little deeper, dragons started appearing in the analysis.
In theory, goalkeepers influencing shot-on-target rates would do so for shots closer to goal as they would narrow the amount of goal they can aim for via their positioning. However, I found the exact opposite. Further investigation of the model workings pointed to the problem – the model showed significant biases depending on whether the shot was inside or outside the area.
This is shown below where actual and expected shot-on-target totals for each goalkeeper are compared. For shots inside the box, the model tends to under-predict, while the opposite is the case for outside the box shots. These two biases cancelled each other out when looking at the full aggregated numbers (the slope was 0.998 for total shots-on-target vs the expected rate).

Actual vs expected shots-on-target totals for goalkeepers considered in the analysis. Dashed line is the 1:1 line, while the solid line is the line of best fit. Left-hand plot is for shots inside the box, while the right-hand plot is for shots outside the box. Data via Opta.
The upshot of this was that goalkeepers performing well-above expectation were doing so due to shots from longer-range being off-target when compared to the expected rates for the model. I suspect that the lack of information on defensive pressure is skewing the results and introducing bias into the model.
Now when we think of Buffon and Oblak performing well, we recall that they play behind probably the two best defenses in Europe at Juventus and Atlético respectively. Rather than ascribing the over-performance to goalkeeping skill, the effect is likely driven by the defensive pressure applied by their team-mates and issues with the model.
Exploring model performance is something I’ve written about previously and I would also highly recommend this recent article by Garry Gelade on assessing expected goals. While the above is an unsatisfactory ending for the analysis, it does illustrate the importance of testing model output prior to presenting results and testing whether such results match with our theoretical expectations.
Knowing what questions analytics can and cannot answer is a pretty useful thing to know. Better luck next time hopefully.